photofly wrote:I showed it for the 182; you want me to repeat it and see if it's true for the 172 also?

No, you showed me some silly pictures, without any math, or correct theory to substantiate your claim of "tail lift"

I now remember why I dont post on this forum..

To the extent that aerodynamics is just maths and physics, then yes

So the actual hands and feet of piloting of a plane is mostly managing the inertia and aerodynamics of the plane, and that's just maths and physics too?

Why then do we need people who are experienced pilots and aerodynamicists? We can just rely on math and physics experts to take care of those roles, perhaps with minimal aviation experience!

Happily, my 38 years of flying planes, and increasingly understanding why and how they fly, cannot be overturned by anonymous self professed math and physics experts on a public internet forum. I sure hope that other readers here are appropriately wise and cautious.

I suppose photofly, and dr.areo we'll have to just disagree. I simply do not believe that you have made a persuasive argument to support your mysterious beliefs. Many of the facts and applicable design requirements I have presented have gone by unaddressed by you - and they are the real world, final facts, to which all certified aircraft conform. I am not a math or physics whiz, and some of the formulae pass by me in a mist, but I have flown these planes for decades, and had a lot of experiences on the edge of safe, including some surprising and foolish ones to do with loading, controlability, and stability. I have done many of test flights in accordance with the procedures for a Transport Canada flight test program, and recorded and documented actual pitch control data - one graph of which has appeared here to support what I say. Neither of you has risen to describe how the results I recorded and presented, relate to a certifiable airplane. They represent exactly the non compliant conditions you promote as normal, I would think that you'd be hanging your hats on them!

Within the first 18 seconds of this NASA video, the facts are made clear about what a tail does....



When you have flown such an aircraft in a controlled environment, and recorded similar results, please document them, and bring them back here for a real world discussion.

In the mean time, for heaven's sake, all the other pilots reading all of this, please depend upon the formal training you have had, and supplement it with authoritative information. Some of what can be read on the internet is simply blindly wrong.

In the mean time, for heaven's sake, all the other pilots reading all of this, please depend upon the formal training you have had, and supplement it with authoritative information. Some of what can be read on the internet is simply blindly wrong.

Best advice in this entire thread.

..

double

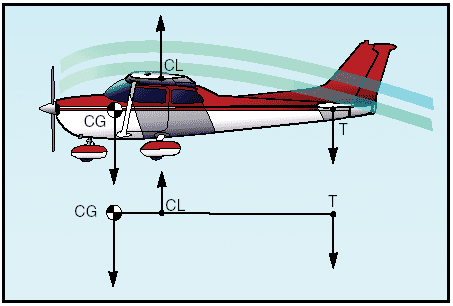
All this bitchin' makes you all look very unattractive.

Strega wrote:No, you showed me some silly pictures, without any math, or correct theory to substantiate your claim of "tail lift"

OK here's a more formal version then.

Let's start with Von Mises' Theory of Flight (Dover, 1959) eqn. (35) in Section XVII.5.
http://books.google.ca/books/about/Theo ... edir_esc=y

I adopt his notation, although the working is mine.

That is, with:

M0 the pitching moment of the wing
M'0 the pitching moment of the tail
Mf the pitching moment of the fuselage
Mp the pitching moment of the propellor thrust
L the lift of the wing
L' the lift of the tail (both lifts positive when lifting upwards)
x_a the horizontal distance from the cg to the aerodynamic centre (ac) of the wing
x'_a the horizontal distance from the cg to the ac of the tail
M the total moment
W the weight of the aircraft

(We follow convention and say that positive moments are in the nose-up direction.)

M = M0 + M'0 + x_a.L - x'_a.L' + Mp + Mf --(1)

The equilibrium condition is that M = 0

and also we have

L + L' = W --(2)

That is, the sum of the lifts = the weight of the aircraft.

The tail airfoil is symmetric, therefore M'0 = 0
We consider the case where the engine is idling, therefore thrust is zero and Mp = 0

Mf, the pitching moment of the fuselage (and undercarriage) is hard to determine. Von Mises says it has the same order of magnitude and direction as the M0, the wing moment. He also says (p.513) that if the aircraft flies parallel to the longitudinal axis of the fuselage that Mf is zero. We'll consider this to be the case, although we note for a C182 the fixed undercarriage is an obvious source of asymmetry.

Then from (1) and (2):

0 = M0 + x_a.(W-L') - x'_a.L'

gathering terms in L' etc:

L' = (M0 + x_a.W) / (x'_a + x_a) --(3)

We're interested in the sign of L'. If it's positive then the tail lifts; if L' turns out to be negative then the tail applies a downforce.
The denominator of the r.h.s. of (3) is positive, so L' takes the same sign as the numerator:

L' > 0 ⟺ M0 + x_a.W > 0

What's the significance of this condition? It's exactly where I started, in the so-called "silly" diagram, except taking moments about the ac instead. M0 is the pitching moment of the wing about the ac, and x_a.W is the moment generated by the weight of the aircraft acting about the ac. M0 is negative for a wing with positive camber. If the magnitude of M0 is sufficient to overcome the weight acting at the cg then the tail is required to resist a nose-down moment, and therefore generates a down-force; L' will turn out to be negative.

On the other hand, if the magnitude of M0 is insufficient to counterbalance the weight of the aircraft acting about the ac, then the tail force will be positive, to hold the nose down.

What values do M0, x_a, and W take? Let's look at the C182, and here's the NACA data for the 2412 airfoil:
http://www.tricity.wsu.edu/htmls/mme/me ... ca2412.jpg

x_a is the distance from the ac to the cg. The ac is at 0.239-0.247 mac, close to station 37" as per the "silly" diagram. The cg at it's rearmost limit is at 48.5". So x_a has a maximum value of (48.5 - 37) = 11.5". W is the weight whose maximum value is 2950 lbs.

X_a.W is therefore a nose-up moment of, in the worst case, 2827 ft.lbs.

The pitching moment coefficient about the ac, Cm_ac, is close to -0.045 (thanks to Steve Pomroy for the data, noting your typo in your post, Steve). The moment itself is obtained from the equation for pitching moment coefficient:

M = q.S.c.Cm

where q is the dynamic pressure, S the wing planform area, c the chord and Cm the coefficient of pitching moment.

Again, for the C182, S = 174sq.ft, c = 5ft
At a speed of 100kts, 1atm, 59°F, q = 0.24 psi or 33.9 lbs/sq.ft
M0 = -1327 ft.lbs


Then M0 + x_a.W = 1500 ft.lbs, which is positive, and so the tail lifts.


Note that X_a.W is more than twice M0 - the pitch down moment of the wing is less than half that of the pitch-up moment of the weight of the aircraft, and that the difference is provided by that tail lift.

PIlotDAR wrote:Neither of you has risen to describe how the results I recorded and presented, relate to a certifiable airplane.

Er, yes, actually, I did. I told you to read up on the stick free neutral point. That's where your problem lay.

They represent exactly the non compliant conditions you promote as normal, I would think that you'd be hanging your hats on them!

38 years of piloting doesn't seem to help you read and understand what someone else writes, when your real desire is just to argue instead. I will try one more time.



I'm sorry you had stability problems. Stability problems arise when the cg moves rearward. Lifting force on the tail is a condition for equilibrium that also happens when the cg moves rearward. That doesn't mean that lifting force on the tail causes stability problems.

To try to make that point that these are separate issues even clearer: http://en.wikipedia.org/wiki/Correlatio ... _causation.




There is a point such that if you move the cg aft of it, you get stability problems (two points actually, one for stick fixed, and one for stick free.) They are called the neutral points. These points are about pitch stability.

There is another point such that if you move the cg aft of it, you get a lifting force on the tail. It is called the centre of pressure. This point is all about pitch equilibrium.

These points do not occur at the same place. These effects do not happen with the cg at the same place. They are different. Different.





This is not a discussion about stability. It's a discussion about equilibrium. Stability and equilibrium are two different things. I've said it about a dozen times in this thread, it's still the point you're missing, and it's still true.

If you see a flaw in my argument then I'm all ears to hear it. But this "sucks-yahboo, I've 38 years of experience therefore you must be talking tosh" line of argument doesn't do you any credit.

PilotDAR wrote:Were the force which the horizontal tail exerts around the pitch axis to change from a downward force to an upward force ("lifting"), the pilot would experience control reversal, which is extremely disconcerting, and not approvable.

It would result in very unpleasing stall handling characteristics, and be graphed something like this,

(The reference to "pounds" is control force measured in pitch, with "-" being a push force.)

(and "Tq" is the % engine power being produced)

which I recorded during a flight test in a Cessna like derivative aircraft. This was definitely not certifiable, and downright scary when I first experienced it during takeoff.

PilotDAR wrote:Sec. 23.173

Static longitudinal stability.

Under the conditions specified in Sec. 23.175 and with the airplane trimmed as indicated, the characteristics of the elevator control forces and the friction within the control system must be as follows:
(a) A pull must be required to obtain and maintain speeds below the specified trim speed and a push required to obtain and maintain speeds above the specified trim speed. This must be shown at any speed that can be obtained, except that speeds requiring a control force in excess of 40 pounds or speeds above the maximum allowable speed or below the minimum speed for steady unstalled flight, need not be considered.

That requirement is applicable to all C of G positions

PilotDAR wrote:It's not the force on the elevator control, but the change in force per change in G (with no change in trim) which matters

I think the disconnect in this conversation is that PhotoFly is talking about moments on the whole aircraft to establish equilibrium, but PilotDAR is talking about control forces -- which are related to but not the same thing as stability. Control forces are determined by the hinge moment. For a given tail load, the hinge moment can be varied by changing the size or geometry of the elevator horn, shifting the hinge position, readjusting the trim tab, re-gearing the servo- or anti-servo tab, etc. The certification standard quoted above ultimately pertains to hinge moment requirements. These hinge moment requirements can be met (or violated) regardless of the direction of the load on the tail.

Strega wrote:fyi most airplanes I fly,, you have to pull back "hard" to make them stall....

Once again, hinge moment, not tail force.

photofly wrote:So my range of CG's for which the tail lifts should read about 39" to 48.5" (depending on airspeed).

Do you agree with the calculation?

I haven't checked your numbers, but your approach seems valid at first blush. I will qualify that again though, with the fact that we are ignoring the (possibly significant) effects of the fuselage and engine.

photofly wrote:Bill Crawford, who wrote that document, runs an unusual attitude training course, with an academic ground school attached. Who's up for a trip down to Plymouth?

Sign me up! That course has been on my wishlist for ages.

I have said very early on that I lack the academic qualification to engage in a math based discussion, and that remains the case. I admit to an unwillingness to devote myself to learning enough math to apparently refute all the teaching and experience I have received all these years of flying.

I do respect the role of a competent aircraft designer to design an aircraft, and understand things about it which I do not. I have no idea about the competence of others here with whom I disagree, but the math looks impressive. So yes, I would fly the plane you design with the lifting tail, but with great caution as I probe the limits of its safe capability.

Nothing in the foregoing should encourage anyone to fly their aircraft "differently" or outside its limitations, nor teach flying differently than conventional norms provide for, other than perhaps to acknowledge that there could be factors out side the norm, around the edges which conflict with conventional thinking. Those are accounted for in the certified aircraft design, so think about them if you like, but fly the plane as it was approved.

With that, I concede that I might have learned something here, though I'm not sure what, and it will not affect the way I fly planes.

I will qualify that again though, with the fact that we are ignoring the (possibly significant) effects of the fuselage and engine.

Evidence that the thrust doesn't play a huge role: that (flaps up) the pitch change with power is relatively small and what pitch change there is seems mostly to come from increased downwash over the tail.

For the wheels, likewise: I've not flown a 182RG but for a 177RG the pitch change as the undercarriage is raised and lowered is limited and I imagine the 182RG is similar.

I agree that the fuselage pitching moment is the big unknown. When I get my 182 back I'll stick some tufts on the stab and see which way they spin with different cg positions (within the approved envelope.)

PilotDAR wrote: Nothing in the foregoing should encourage anyone to fly their aircraft "differently" or outside its limitations, nor teach flying differently than conventional norms provide for, other than perhaps to acknowledge that there could be factors out side the norm, around the edges which conflict with conventional thinking. Those are accounted for in the certified aircraft design, so think about them if you like, but fly the plane as it was approved.

Of course not. I don't think anybody claimed you should fly those airplanes differently. On the contrary, the point is that you won't even notice if your tailplane generates lift or not.

With regards to the teaching: as is often the case in sciences (physics, chemistry) and to a lesser extent in mathematics, is that what they teach is basically correct, but only for specific cases. It's one way of teaching it, without the need to resort to "difficult" mathematics (integrals, differential equations etc) that would cover all options. It gives you an easy to read schematic that allows to explain the theory, but only one side of the theory.

For example the basic explanation of how a wing works: no aviation textbook I ever read explained it completely and correct. There are always some loose ends (or even errors) in their explanation. But the explanation does help to have some understanding, or to at least get you to agree that it works "a little bit similar like this".

The more mathematics you know, the more complete your theory gets, and more accurate it is. The downside of it, sometimes, is that it causes you to start doubting the very basic things, or you start to work so theoretical that you lose sight of the reality.

This is most clearly visible in the chemistry courses you probably got in secondary school (or is it called high school in Canada ? Anyway,...). They explain something basically, give a few examples, add another rule , add exceptions, add exceptions to the exceptions etc. It makes you wonder how any chemical substance would ever be created. While the truth is, if you know the full theory with all the difficult equations, it all makes sense and you can predict everything that will happen. The rules / exceptions / exceptions on the exceptions are created to explain some chemistry to people new to the field and without sufficient mathematical knowledge.

It would be like learning someone to fly without explaining or using the word 'wing'. He would probably learn it after a while by pressing the buttons you tell him to, however, he would probably never understand the things like slow flight, stalls, induced drag etc.

----

When I reread the text above, it sounds like I pretend to know everything. This is not the case . I do not know all these "general theories" I mentioned above. I did, however, learn enough to know that hey exist.

For those who like to know: I have a university degree in engineering (electronics) and had some courses on airplane aerodynamics. No practical experience in those areas except for flying 'normal small planes'.

The figures above aren't for a new experimental aircraft; they're for the C182, which is the world's second most popular aircraft (after the C172). And I'm not designing an aircraft, just doing some basic algebra on one that's already designed.

Let's ask how the cg position at which the tail starts to lift varies with speed: this is through the connection of speed and dynamic pressure.

We saw that L' > 0 ⟺ M0 + x_a.W > 0

Let's look at the condition

M0 = x_a.W -- (4)

Which means the aircraft is in balance without the tail. That is, we still need the tail to provide stability but it provides no force while the aircraft is in equilibrium.

M0 = q.S.c.Cm
q = 1/2 . rho. v^2

Therefore

(rho . v^2 . S . c . Cm )/2 + x_a.W = 0, for some v, we call v_crit

rearranging:

v_crit = [ (-2 . x_a . W) / (rho . S . c . Cm) ] ^ (1/2)
Note that Cm is negative so the term in the square bracket is positive, and has a real square root.

being extremely careful with units, and using the correct physical quantities (I think) we get:

v_crit = 41.2 √x_a (v in knots, x_a in inches)

x_a is the distance from the cg to the ac. As before, the ac is at chord/4, at 37", and the cg range is 33 - 48". So we could write instead

v_crit = 41.2 √(cg - 37") where again we measure the cg in inches aft of the firewall, and v is in knots.

When v > v_crit, the dynamic pressure is sufficient for the nose-down pitching moment from the wing to require a downforce on the tail. If v < v_crit, the rearward cg overcomes the pitching moment from the wing and for equilibrium the tail is required to lift.

Does the physical form of this limit make sense? Yes: if the speed is very low then then the angle of attack is high and the centre of pressure is forward, nearest to chord/4. It's easy to move the cg aft of the cp whereupon the tail lifts. On the other hand if the speed is high then the angle of attack is low: the cp moves rearwards, the dynamic pressure increases, the wing moment increases and we increase the downforce required by the tail to resist.

If the cg is forward of the chord/4 then it is always forward of the centre of pressure, and the tail supplies a down-force at all speeds: the operand of the square root in the expression for v_crit is negative and so has no real root.

Here's how I think that works out, in graphic form, for all speeds between stall and redline, and for cg between the front and rear limits, at maximum weight: As usual, corrections to my math or analysis are gratefully accepted.

EDIT: having gone through the figures I think I had them wrong the first time. This is an adjusted graph.

PF: You and Liquid Charlie, like teenaged girls, have
to learn to stop giving it away for free!

Colonel Sanders wrote:PF: You and Liquid Charlie, like teenaged girls, have
to learn to stop giving it away for free!

Teenaged girls have a well-proven path towards monetization.

I suppose you're right. For every ex-wife who is an
excellent house-keeper, there was probably once a
teenaged girl that gave it away for free.

PilotDAR wrote:It would result in very unpleasing stall handling characteristics, and be graphed something like this, ...
which I recorded during a flight test in a Cessna like derivative aircraft. This was definitely not certifiable, and downright scary when I first experienced it during takeoff.

Ok, I'm curious. What was the fix here? Or was the project abandoned?

Photofly, Dr. Aero, and anybody else for that matter.

Since this is a flight training forum how about a post on how you think I, a working part time instructor, should teach "what the tail does" to a PPL, a CPL ?

What the tail does:



As C of G moves aft, aircraft gets faster because
tail creates less drag. Unpleasant to fly.

Next question?

photofly wrote: As usual, corrections to my math or analysis are gratefully accepted.

Great and clear post! Maybe you could add some airframe moments yourself (what would be realistic) and see how the curve moves in function of these moments.

Colonel Sanders wrote:What the tail does:



As C of G moves aft, aircraft gets faster because
tail creates less drag. Unpleasant to fly.

Next question?

No No.. It lifts... didnt you see pf's explanation

Maybe i should open up a can of worms and ask this : Does a wing create lift by the reduced pressure over the wing or by the downflow of air (directional change) past the wing or both ?

Yes.

Strega, how does an aircraft like this maintain stability?




Do you believe that this front-engined aircraft is supporting its whole weight on those stubby wings in front, plus the downforce from those wings in the back? I sure hope the pilot has someone to hold the tail down when he gets out of the aircraft!

Thanks for the wikipedia article though... it says the same thing I was saying when I said this.

The only exception is during stall when the C of L moves rearward.

I can quote the internet too... so when you disagreed with this..

Propeller blades do the same thing.

I can show you this.

http://www.datwiki.net/page.php?id=248& ... rching=yes

Not that it applies to a wing attached to an airplane because the point of rotation is in the C-of-G, not a hub bearing... but again, you brought it up in a poorly worded response. I thought we had covered that in the beginning, and I added the thrust-drag couple... what else was there to add?

Back to C of L... I gave you an opportunity to give in a little bit, but it's time for more internet.







Which supports what I said.

It is not supportive of increasing the downforce on the tail of the aircraft.

Because of the decreasing distance between C of L and the C of G.

So..... is the C of L moving backwards really required for any increase in angle of attack for longitudinal stability? Or can it just move rearward close to the stall? Remember, we are just cruising along, not anywhere near the stall. With a tail exerting lots of authority maintaining a positive angle of attack on the wings... what is going to cause the aircraft to go tumbling out of control should it happen to be lifting rather than pushing?

Again, I have no idea whether it is even possible for an aircraft like a 182 to lift up on the tail, but when you see aircraft like the Quickee and a zillion canard aircraft that have lift over all of their surfaces, it makes it hard for me to believe that it is impossible.